✏️ 문제

문제 파악
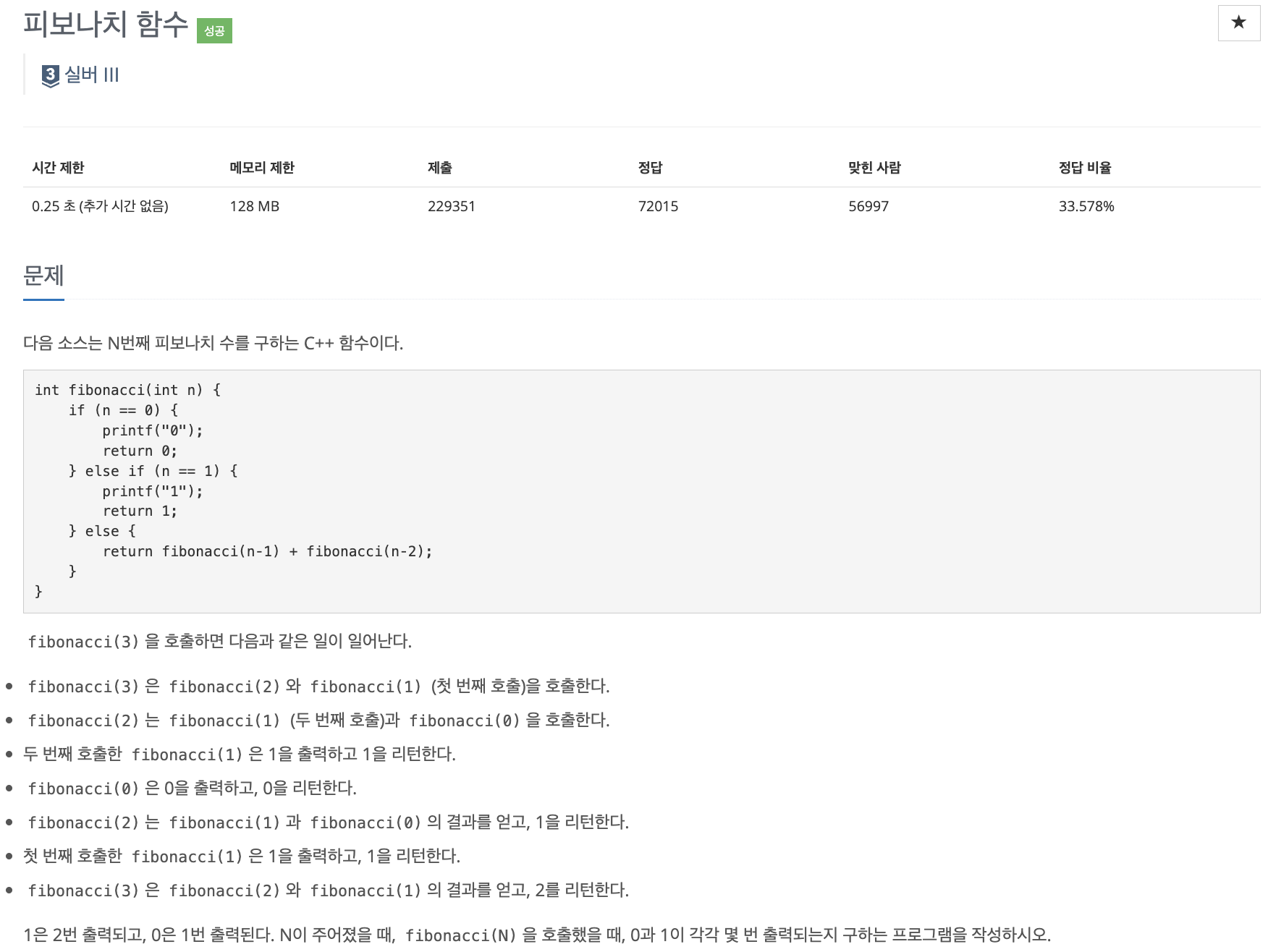
피보나치 수열은 f(n) = f(n-1) + f(n-2) 이다.
이는 즉 f(n)의 f(0) 호출 횟수과 f(1) 호출 횟수는 f(n-1)의 f(0) 호출 횟수과 f(1) 호출 횟수 + f(n-2)의 f(0) 호출 횟수과 f(1) 호출 횟수 라는 것을 의미한다.
직접 값을 찾아보면 다음과 같이 나온다.
| n | f(n) | f(0) 호출 횟수 | f(1) 호출 횟수 |
| 2 | f(2) | 1 | 1 |
| 3 | f(3) | 1 | 2 |
| 4 | f(4) | 2 | 3 |
| 5 | f(5) | 3 | 5 |
| 6 | f(6) | 5 | 8 |
위의 표를 보면
- f(n)일 때, f(0) 호출 횟수 = f(n-1)의 f(0) 호출 횟수 + f(n-2)의 f(0) 호출 횟수
- f(n)일 때, f(1) 호출 횟수 = f(n-1)의 f(1) 호출 횟수 + f(n-2)의 f(1) 호출 횟수
이전에 설명한 것과 같이 값이 잘나온다.
이 점화식을 활용하여 코드를 짜면 쉽게 풀 수 있다!
알고리즘
- 다이나믹 프로그래밍
코드
for _ in range(int(input())):
n = int(input())
dp = [[]] * 41
dp[0] = [1, 0]
dp[1] = [0, 1]
dp[2] = [1, 1]
for i in range(3, n+1):
dp[i] = [dp[i-1][0] + dp[i-2][0], dp[i-1][1] + dp[i-2][1]]
print(dp[n][0], dp[n][1])
'PS > 백준' 카테고리의 다른 글
| [Python] 1149번 RGB거리, 문제 완벽 분석!! 그림 설명 (1) | 2024.09.11 |
|---|---|
| [Python] 9095번 1, 2, 3 더하기 (1) | 2024.09.07 |
| [Python] 6118번 숨바꼭질 (2) | 2024.09.05 |
| [Python] 13565번 침투 (0) | 2024.09.05 |
| [Python] 2210번 숫자판 점프 (1) | 2024.09.02 |