728x90
반응형
SMALL
힙(Heap)은 트리 기반의 자료구조로 특정한 규칙(힙 속성)을 만족하는 이진 트리이다.
힙은 동적으로 변하는 데이터에서 최댓값 또는 최솟값을 빠르게 찾고 관리하기 위해 생겨났으며 데이터 삽입 및 삭제 시 힙 속성을 유지하는 것이 핵심이다.
이러한 힙 속성 덕분에 삽입, 삭제 시에도 효율적으로 동작하며 우선순위 큐와 같은 문제를 효과적으로 해결하기 위한 자료구조로 발전했다.
1. 힙의 특징
힙은 배열로 구현 가능하여 메모리 효율적이지만 정렬된 상태로 데이터를 저장하지 않는다는 특징이 있다.
1.1 완전 이진 트리 (Complete Binary Tree)
힙은 항상 완전 이진 트리 형태를 유지한다.
마지막 레벨을 제외한 모든 레벨이 꽉 차 있어야 하며 마지막 레벨은 왼쪽부터 채워져야 한다.
1.2 힙 속성 (Heap Property)
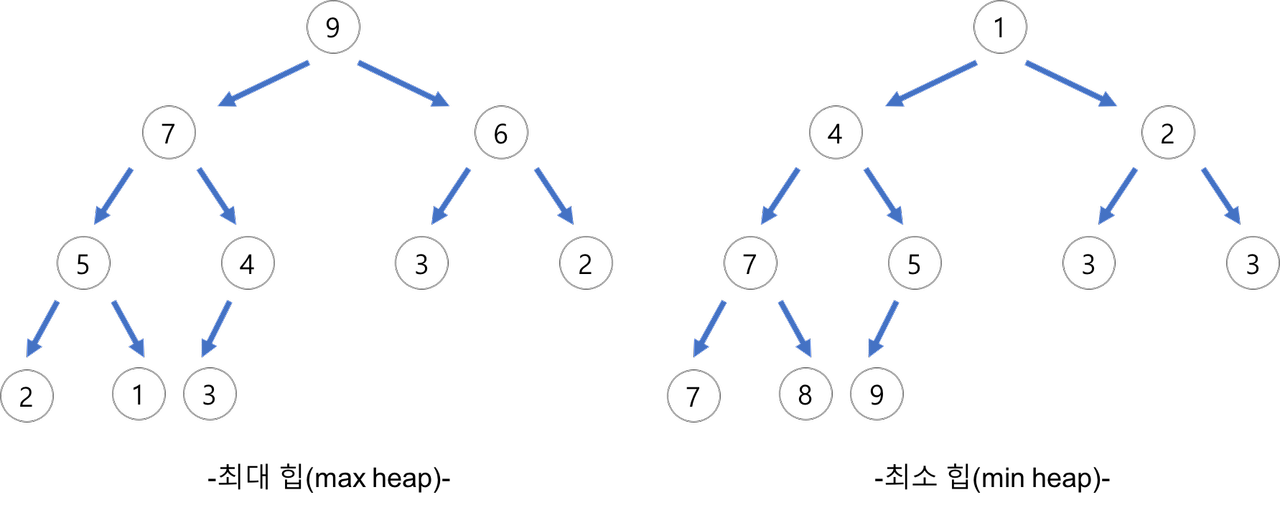
- 최소 힙(Min-Heap): 루트 노드가 트리에서 가장 작은 값이며 부모 노드의 값이 항상 자식 노드의 값보다 작거나 같다.
- 최대 힙(Max-Heap): 루트 노드가 트리에서 가장 큰 값이며 부모 노드의 값이 항상 자식 노드의 값보다 크거나 같다.
1.3 시간복잡도
| 연산 종류 | 시간복잡도 |
| 최댓값 또는 최솟값 조회 : 루트 노드에 바로 접근 가능하다. |
O(1) |
| 삽입 및 삭제 연산 : 트리의 높이가 log n이므로 한 번의 삽입이나 삭제는 트리 높이만큼 연산한다. |
O(log n) |
| 특정 값 검색 : 일일이 찾아봐야 하므로 n번을 돌아야 한다. |
O(n) |
list(배열)의 삽입 및 삭제, 특정 값 찾기가 최악일 때 O(n)인 거에 비해 훨씬 작은 시간복잡도를 가지고 있다.
1.4 실제 활용
힙은 다양한 알고리즘과 문제 해결에 활용된다.
- 힙 정렬 (Heap Sort): 힙을 이용하여 배열을 오름차순 또는 내림차순으로 정렬
- 우선순위 큐 (Priority Queue): 힙을 기반으로 효율적인 우선순위 큐 구현
- 최단 경로 알고리즘: 다익스트라 알고리즘에서 우선순위 큐로 사용
- K번째 최댓값/최솟값 찾기: 힙을 사용하여 효율적으로 K번째 값을 찾음
- 스트림 데이터 처리: 동적으로 데이터의 최댓값, 최솟값을 추적
2. 힙의 배열 구현
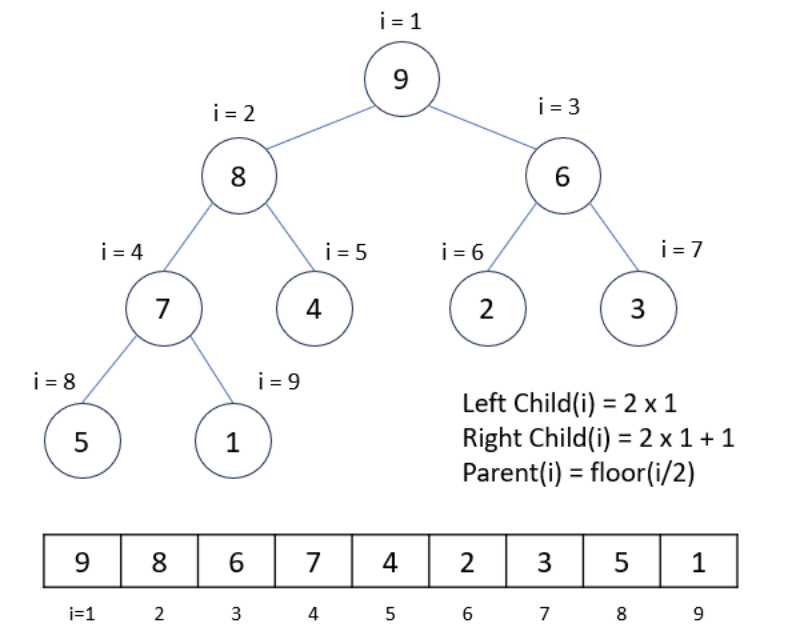
힙은 트리 구조이지만 배열로 효율적으로 구현할 수 있다.
배열에서 인덱스를 이용하여 부모-자식 관계를 나타낸다. 이때 구현을 쉽게 하기 위하여 배열의 첫 번째 인덱스인 0은 사용되지 않는다.
- 부모 인덱스: i
- 왼쪽 자식: 2i+1
- 오른쪽 자식: 2i+2
- 부모 노드: ⌊(i−1)/2⌋
3. 힙의 주요 연산
3.1 삽입 (Insert)
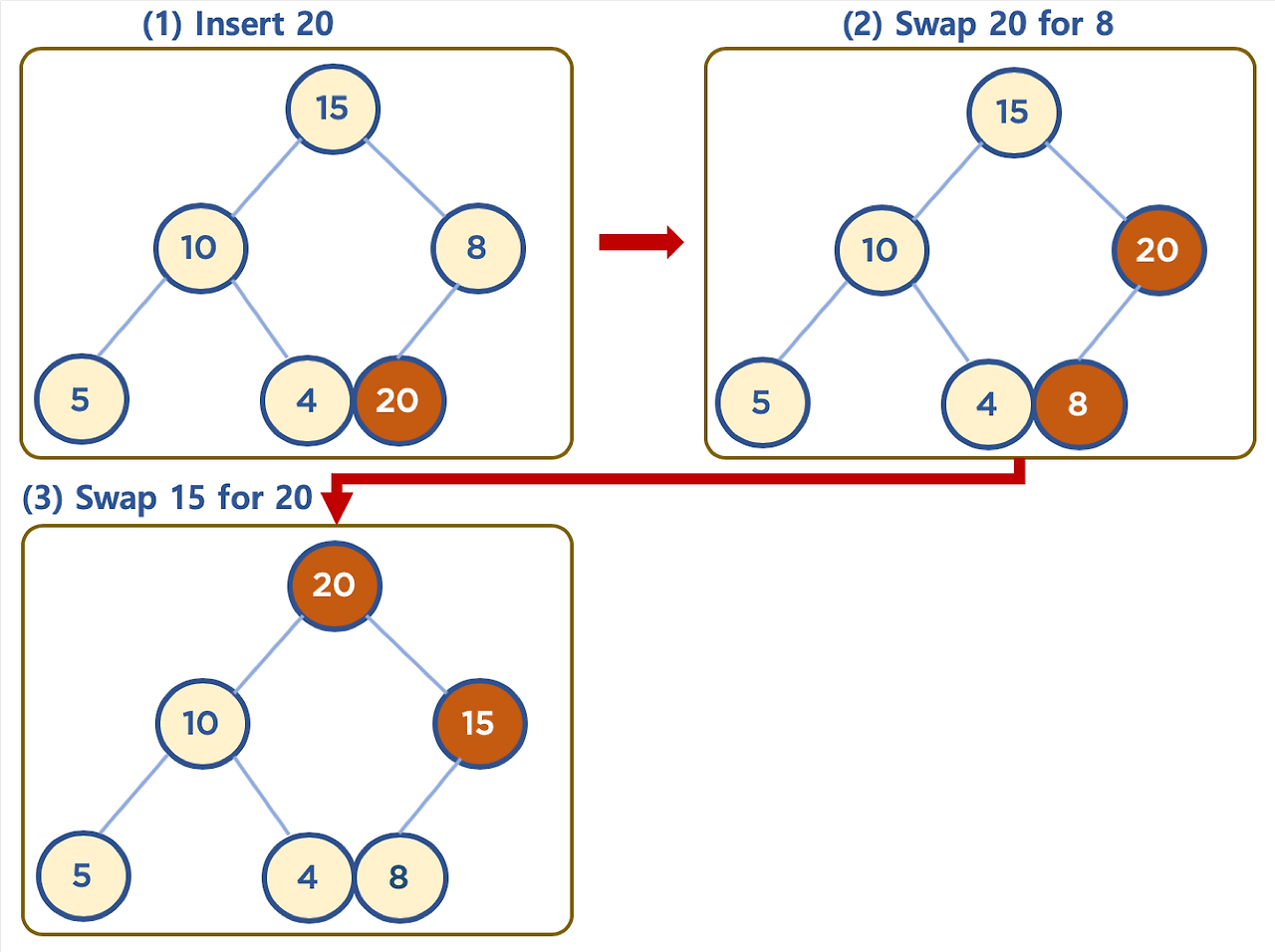
새로운 데이터를 힙에 삽입할 때 완전 이진 트리 형태를 유지하면서 힙 속성도 만족해야 한다.
- 새로운 데이터를 트리의 가장 마지막 위치에 삽입한다.
- 부모 노드와 비교하여 필요하면 위치를 교환(Up-Heapify 또는 Bubble-Up)한다.
- 루트 노드까지 반복한다.
3.2 삭제 (Delete)
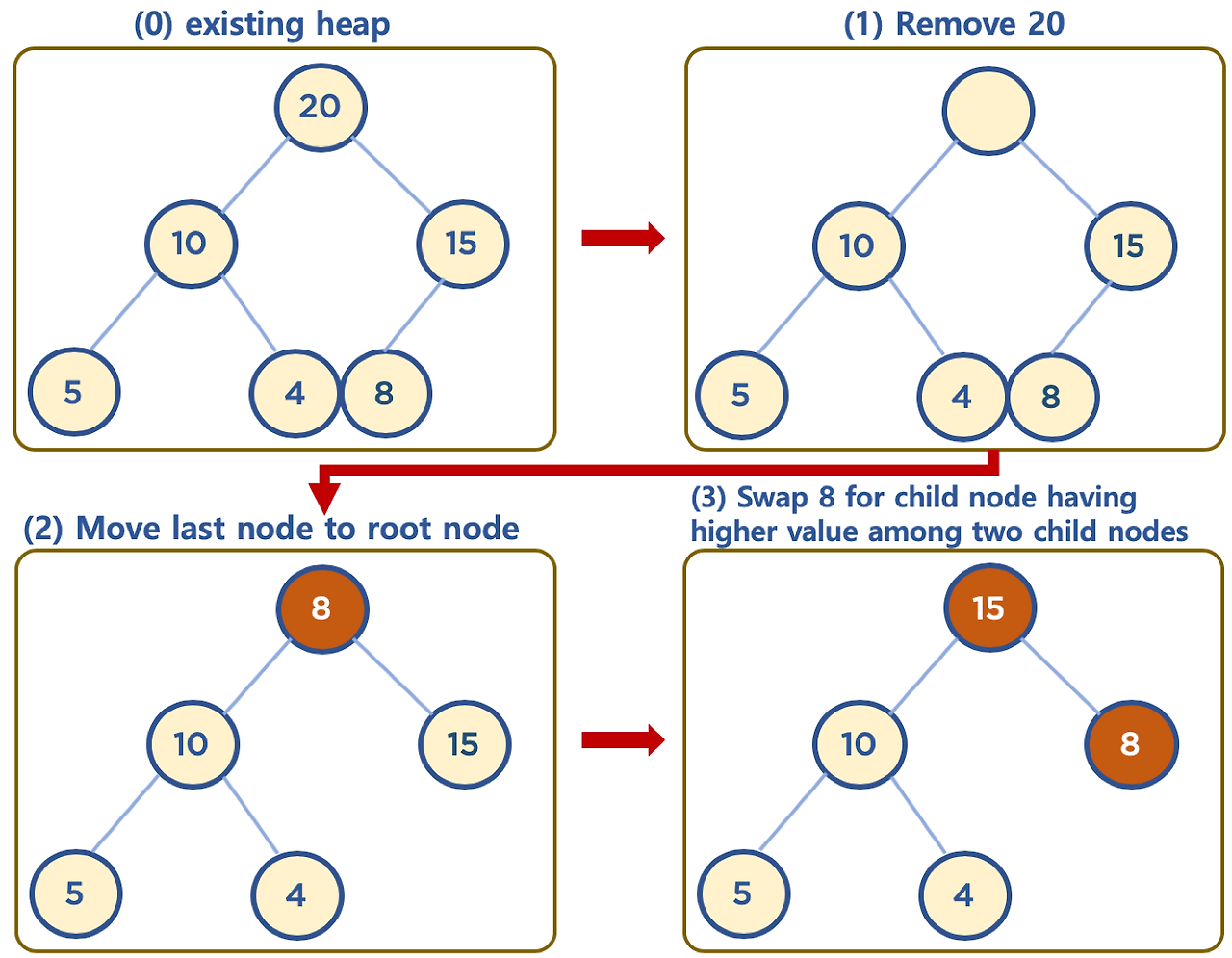
힙에서 데이터를 삭제하면 힙 속성을 유지해야 하므로 보통 루트 노드(최솟값 또는 최댓값)를 제거한다.
- 루트 노드를 삭제하고 마지막 노드를 루트 위치로 이동한다.
- 자식 노드와 비교하여 필요하면 위치를 교환(Down-Heapify 또는 Bubble-Down)한다.
- 리프 노드까지 반복한다.
728x90
반응형
LIST
'알고리즘' 카테고리의 다른 글
| [알고리즘] 카데인 알고리즘 (Kadane's Algorithm) (0) | 2024.09.13 |
|---|---|
| [알고리즘] DFS와 BFS (0) | 2024.08.08 |
| [알고리즘] 이분 / 이진 탐색 (Binary Search) 알고리즘 (0) | 2024.07.25 |
| [알고리즘] 그리디 알고리즘 (Greedy Algorithm) (0) | 2024.07.17 |
| [알고리즘] 최대공약수와 최소공배수 구하기, 유클리드 호제법 (0) | 2024.01.30 |